This handout was given our during our presentation at SIGGRAPH '96. For more information, you may look at the slides or send email to Michael Herf or Paul Heckbert
This is a quick overview of how to implement our soft shadows algorithm. We'll discuss both workstation (RealityEngine-level) implementations and PC implementations. For a general overview of how the algorithm works, see our Technical Sketch in the SIGGRAPH 96 Visual Proceedings.
To begin, you'll need some scene geometry to render, and a list of polygons you want to generate realistic shadows for. Keep the latter to a small number if you want good performance - most texture mapping hardware and software we've encountered handles large numbers of independent textures very badly.
Next, you'll need a set of lights to illuminate your scene. The physical geometry of the lights really doesn't matter. What is more important is how well you sample them. You should probably have a sampling function which allows incremental improvements in quality. (e.g., you give it a parameter n and it returns the coordinates, colors, and intensities of n or n2 point light samples.) Our implementation uses only parallelogram light sources, and uses a jittered sampling grid across each one. Whatever you do, use stochastic sampling.
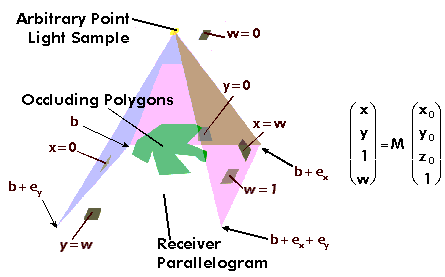
This transformation converts any pyramid
defined by two points a and b (the point light sample
and one vertex of the receiver parallelogram) and two vectors
ex and ey to a unit box.
You need a parallelogram to bound each
of the receiver polygons. For triangles, make the triangle half
of the receiving parallelogram. For general polygons, the simplest
bounding parallelogram is a rectangle. Use the above 4x4 matrix
to transform every vertex in the scene.
Following that, you'll have to clip
against this box: [0, 1] in x, [0, 1] in y, and
[1,
OpenGL provides an accumulation buffer
which allows any linear combination of images. You can use the
RE to compute either modulation textures (grayscale images
which "modulate" an existing texture), or radiance
textures, which accurately depict the diffuse shading from
all of your area light sources. The latter is more interesting,
and the former more obvious, so I'll be describing how to make
radiance textures.
Our implementation decides the size
of a texture for a polygon by choosing a power of 2 (clamped at
256) for each width and height, based on the size of the polygon
in world space. We set a 2D viewport to encompass these chosen
pixels, setting the viewport coordinate system to [0.0, 1.0] for
width and height, and determine a global transformation matrix
using the following code:
[The exact parameters for the glOrtho
call were found by experimentation.] For each light sample, the
target polygon can be subdivided and drawn as a series of triangle
strips, each triangle Gouraud-shaded. If you want an ambient
component in your texture, you can add this image (without shadows)
to your accumulation buffer. Next, all objects should be drawn
without z-buffer, without Gouraud shading, just flat black, on
top of the shaded background. Add this image to the accumulator
after drawing all other objects in the scene. Choose a new light
sample, set a new matrix, and keep going until you've exhausted
your sample points. After that, you have a radiance texture.
Some initial testing indicates that
an implementation of this algorithm could be made to run quickly
on PC hardware. Memory bandwidth is the limiting factor, but
some simplifications to the algorithm can make it speedy.
First, we should only compute modulation
textures during the accumulation steps. If you want colored lights
as well, do this afterwards using one point per light source.
This keeps the depth of the textures to 8 bits, dramatically reducing
the amount of memory bandwidth required to do the compositing
and drawing.
Second, use adds to do the compositing.
With some planning in advance, we don't need an accumulation
buffer 2x as big as the depth we draw to (like OpenGL does).
Choose the number of lights samples n so that n is
a factor of 256-a (for a=ambient intensity). Then,
draw each polygon flat-shaded on a black background with color
(256-a)/n. These techniques (along with fast software
polygon renderers) should make reasonable performance on PCs achievable.
Algorithm Recap/Overview
Preprocessing
Display
Math: Computing the Transform
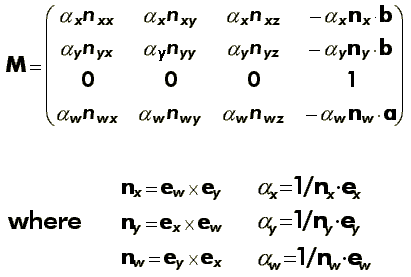
 ] in z. Finally, flatten everything
in z, and you'll have a hard shadow image in x and
y, which you can composite with similar hard shadows.
] in z. Finally, flatten everything
in z, and you'll have a hard shadow image in x and
y, which you can composite with similar hard shadows.
RealityEngine/OpenGL Implementation
make_projmatrix(ourmatrix.a);
// OpenGL stuff
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0.0, 1.0, 0.0, 1.0, -0.999, -1000);
glMultMatrixf(ourmatrix.a);
glMatrixMode(GL_MODELVIEW);
PC Implementation Tips
Michael Herf can be contacted at
herf+@cmu.edu. Paul Heckbert can be contacted at ph@cs.cmu.edu.
What you have just read is a summary of a work in progress, "Simulating
Soft Shadows with Graphics Hardware", PH and MH. For
more information, see
http://www.cs.cmu.edu/~ph.